Hidden Markov Model

HMM

A Markov chain is useful when we need to compute a probability for a sequence of observable events. In many cases, the events we are interested in are hidden - meaning we don’t observe them directly.

HMM allows us to talk about both observed events and hidden events that we think of as causal factors in our probabilistic model.

A HMM is specified by the following components:

• A set of N states

  Q = q1, q2, …, qN

• A transition probability matrix A, each aij representing the probability of moving from state i to state j, such that: ∀i. Σj=1n aij = 1

  A = a11, a12, …, an1, …, ann

• An initial probability distribution over states. πi is the probability that the Markov chain will start in state i. Some states may have πj = 0, meaning that they cannot be initial states. Also, Σj=1n πi = 1

  π = π1, π2, …, πN

• A sequence of T observations, each one drawn from a vocabulary V - v1, v2, …, vv

  O = o1, o2, …, oT

• A sequence of observation likelihoods, each expressing the probability of an observation ot being generated from a state i

  B = bi(ot)

Hidden Markov Model (HMM) is a statistical Markov model in which the system being modelled is assumed to be a Markov process (chain) – call it X – with unobservable (“hidden”) states. HMM assumes that there is another process Y whose behaviour “depends” on X. The goal is to learn about X by observing Y.

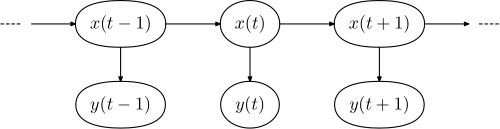
A HMM is specified by two functions (which can be probabilistic):

• A transition function, which defines how to go from hidden state n to hidden state n + 1.
• An observation function, which defines how to go from hidden state n to observed state n.

These functions can be defined in many different ways - there is no generalisation or “typical” implementation. The parameters of a HMM (which we try to learn when inferring a HMM) parameterise the transition function and observation function.

Inference

There are several inference problems associated with HMMs i.e. problems for which we can use HMMs as an inference tool.

• Given the parameters of the HMM, compute the probability of a particular observed sequence
• Given the parameters of the HMM and a sequence of observations y(1),…,y(t), compute the probability of some particular latent variable(s).

Learning

The parameter learning task of HMMs is, given an observed sequence, find the best set of state transition and emission probabilities. The task is usually to derive the maximum likelihood estimate of the HMM’s parameters given the set of observable sequences. However in certain situations, Bayesian inference methods such as MCMC sampling are proven to be favourable over finding a single likelihood model.